"A designer knows he has achieved perfection not when there is nothing left to add, but when there is nothing left to take away."
- Antoine de Saint-Exupery
The story begins with a minimal Centos 6.9 installation as usual. I have already explained installation and other steps several times in previous articles. The installation is also out of scope of current post. Therefore, I assume that a machine is already installed.
 |
| yum install gcc gcc-gfortran |
I have updated the machine with yum update command and rebooted as soon as the machine is installed. This step is not strictly necessary but nice to have. I installed gcc and gcc-gfortran packages using yum.
Then, I downloaded LAPACK library. This is an abbreviation for Linear Algebra Package. It is developed with Fortran and contains functions for important matrix operations like, solutions of linear equations, least squares, eigenvalue/eigenvector calculations or matrix factorization algorithms. These functions are not limited to the operations above. They are just what I could remember after graduation. Although we don't encounter those programs based LAPACK in everyday life, many scientific calculation programs are based on this library.
Then, I downloaded LAPACK library. This is an abbreviation for Linear Algebra Package. It is developed with Fortran and contains functions for important matrix operations like, solutions of linear equations, least squares, eigenvalue/eigenvector calculations or matrix factorization algorithms. These functions are not limited to the operations above. They are just what I could remember after graduation. Although we don't encounter those programs based LAPACK in everyday life, many scientific calculation programs are based on this library.
Another important library is BLAS which is another abbreviation for Basic Linear Algebra Subroutines. It is a lower level library, which provides vector and matrix operations and LAPACK needs BLAS for compilation.
OK, the first thing that needs to be clarified is whether we really need these libraries for a simple matrix multiplication or addition.
I don't really want to dig deep the fundamental definitions and theorems of matrix algebra. I will try to walk around it as much as I can.
So, matrix multiplication is defined on matrices where first matrix has (m x n) and second has (n x p) elements (dimensions). Let's name the first matrix as A and second as B and for simplicity let m = n = p. I mean A and B are square matrices. Let's name the product matrix AB = C, where C is a (p x p) matrix. First row elements of A is multiplied term-by-term with first column elements of B. First element of C is the sum of these p elements.
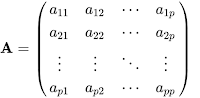 Similarly, second element of C which is on the right of first element consists from the sum of p elements where second row elements of A is multiplied term-by-term with the first column elements of B. I know, it is really confusing to handle this topic verbally. Therefore I am going to define it with mathematical expressions. Let matrix A is defined in the next figure, matrix B is defined in the figure below:
Similarly, second element of C which is on the right of first element consists from the sum of p elements where second row elements of A is multiplied term-by-term with the first column elements of B. I know, it is really confusing to handle this topic verbally. Therefore I am going to define it with mathematical expressions. Let matrix A is defined in the next figure, matrix B is defined in the figure below: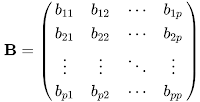
Elements of product matrix C is defined with the formula below:
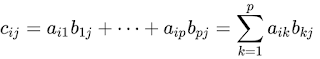
And the positions of individual elements in matrix C is shown below:

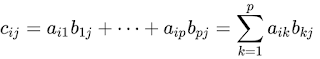
And the positions of individual elements in matrix C is shown below:

If the operation is to be expressed as a pseudo-code, it is as follows:
for i = 1 to p
for j = 1 to p
c(i)(j) = 0
for k = 1 to p
c(i)(j) = c(i)(j) + a(i)(j) * b(i)(j)
for j = 1 to p
c(i)(j) = 0
for k = 1 to p
c(i)(j) = c(i)(j) + a(i)(j) * b(i)(j)
The computational complexity of this operation depends on the third power of p and it is expressed as O(n3) with big O notation. In other words, if two (p x p) matrices are multiplied in unit time, then two (2p x 2p) matrices are multiplied in eight unit time. In literature, different approaches has been developed for this operation and the computational complexity is reduced to O(n2.37) by now. (Further reading: Matrix multiplication algorithm).
The facts with coding and optimization in matrix multiplication is quite different from the theory. For example the pseudo-code above is not optimal because of the cache memory utilization of row-major-order arrays in C. This is an introductionary example of every scientific computation and numerical algorithms lecture. Having the indices with (i, k, j) order provides far better cache hit ratio than the indices with (i, j, k) order. In other words, more operation is done in cache memory and algorithm works faster.
I had researched these algorithms while I was in university. First, I had started with an algorithm similar to the example above and then improved cache usage with reordering indices and keeping the data close to the processor. Then I implemented Strassen Algorithm to the code. As a third step, I applied this algorithm recursively and optimized my code to its theoretical limits. I also utilized compiler optimizations during compilation and reached to a limit in computation time.
Then I multiplied same matrices with BLAS for comparison. I used same compiler parameters while compiling the library and unfortunately BLAS was still about 1/5 times faster than my algorithm (i.e. 4 seconds instead of 5). Even more sadly, two matrices, that are multiplied in about 60 seconds using BLAS, were multiplied in a little longer than one second using Matlab. The code of Matlab was written (or optimized) much better for the underlying processor architecture. The processor I have used in this research had SSE2 support and as I divided the number of multiplications done in the matrix multiplication, to the clock frequency of one processor core, the ratio was very close to one. This means, Matlab was utilizing the core so effective that the core was almost doing nothing except multiplication.
In short, these libraries are really needed to accomplish some good results. BLAS is a thirty years old library and developed by hundreds of people since than. It would be unfair to expect better results from a simple research project developed just in a few months.
In BLAS terminology, first level operations are vector vector operations, second level are matrix vector and third level are matrix matrix operations. LAPACK uses BLAS functions and provides more complex functions.
To be honest, I heard the name of these libraries when I was in university. Likewise, many times I have compiled these libraries and programs depending to these libraries as a part of my business. Unfortunately, the use or the applications of the libraries was not taught in lectures. These words were used like Phoenix of the unknown land. I used BLAS in some of my projects when I was in university, and never used LAPACK. Today I think, this is not a positive thing for a lecture when I look at it from the outside.
I will return to the point after a long introduction. Latest LAPACK version was 3.8.0 by the time I write this article. I have downloaded and extracted it.
curl http://www.netlib.org/lapack/lapack-3.8.0.tar.gz > lapack-3.8.0.tar.gz
tar xvfz lapack-3.8.0.tar.gz
Note: I used curl because there is no wget in minimal CentOS.tar xvfz lapack-3.8.0.tar.gz
After extracting Lapack, I changed to the lapack directory, copied example make.inc file which is included in Makefile, to real make.inc file. Then I compiled the targets in Makefile:
cp make.inc.example make.inc
make lib
make blaslib
make cblaslib
make lapackelib
make lib
make blaslib
make cblaslib
make lapackelib
"lib" is for compiling the Fortran code of LAPACK, "blaslib" is for BLAS library bundled with LAPACK. "cblaslib" is C interface of BLAS and
"lapackelib" is C interface of LAPACK. These targets have to be compiled.
printmat() functions dumps the matrix to the screen. Output is Matlab compatible, so I can double check the results with Matlab. I have defined size = 3 in main(). This defines matrix size. With the code below, matrix size can be given from the command line as a parameter.
if(argc > 1) {
size = atoi(argv[1]);
}
size = atoi(argv[1]);
}
Lapack has its own lapack_int integer type. I assigned size to lapack_size which is a lapack_int variable. I will work on matrixA. It is initially equal to matrixB. I will use matrixB at the end for proof. I allocated the matrices with malloc() and filled them with random values. ipiv vector is used for changing the row order (row permutation) of the matrix. It is empty and unused here.
There are three simple matrix operations in this code. First, I have factorized the matrix with LU method using dgetrf() function. According to the naming convention of LAPACK dgetrf() is: first letter 'd' is for double, 's' for single, 'c' for complex and 'z' for double complex. These are the precision of matrix elements. Next two chars 'ge' means, this function is related with general matrices (without a structure). There are other two letter options for symmetric, diagonal, tri-diagonal and triangular matrices. There is a detailed information in LAPACK documentation and its wiki page. Last three letters are the name of function, e.g. trf means triangular factorization in short. Below is the function, which does the LU factorization:
There are three simple matrix operations in this code. First, I have factorized the matrix with LU method using dgetrf() function. According to the naming convention of LAPACK dgetrf() is: first letter 'd' is for double, 's' for single, 'c' for complex and 'z' for double complex. These are the precision of matrix elements. Next two chars 'ge' means, this function is related with general matrices (without a structure). There are other two letter options for symmetric, diagonal, tri-diagonal and triangular matrices. There is a detailed information in LAPACK documentation and its wiki page. Last three letters are the name of function, e.g. trf means triangular factorization in short. Below is the function, which does the LU factorization:
LAPACKE_dgetrf(LAPACK_ROW_MAJOR, lapack_size, lapack_size, matrixA, lapack_size, ipiv);
In C, two consecutive values of a 2D array is row-wise consecutive in a matrix, like a11 and a12. In Fortan, two consecutive array elements are column-wise consecutive like a11 and a21. If LAPACK_ROW_MAJOR value is given, function handles consecutive array elements as row members. Following lapack_size arguments are number of rows and columns of the input matrix and matrixA is the pointer of the input matrix. Next lapack_size argument is known as LDA, i.e. "Leading Dimension of Array". This value is important when only a submatrix of matrixA is processed. As I will apply the operation to whole matrix, this value should be equal to matrix size (I am going to explain this in the appendix in order to avoid confusion). I gave the zero vector ipiv as the last argument.
After that, I will apply inverse operation to the matrix I had factorized above.
After that, I will apply inverse operation to the matrix I had factorized above.
LAPACKE_dgetri(LAPACK_ROW_MAJOR, lapack_boyut, matrisA, lapack_boyut, ipiv);
'tri' means triangular inverse. I did not want to cover algebra topics but here is a short explanation: The identity element of multiplication in real numbers is 1. A real number multiplied by 1 equals the number itself. An (multplicative) inverse of a number is a number which where two numbers are multiplied, the result yields to identity element. In general, the multiplicative inverse of a real number x is 1/x and each real number except zero has a inverse. These rules are almost valid for the matrices (there are some exceptions). The identity element of matrix multiplication i.e. identity matrix consists from ones in the diagonal and zeroes elsewhere. Not all but many matrices have a multiplicative inverse. (A note for curious minds: https://proofwiki.org/wiki/Matrix_is_Invertible_iff_Determinant_has_Multiplicative_Inverse, bonus: https://proofwiki.org/wiki/Real_Numbers_form_Ring)
Because, only square matrices can have an inverse (actually it's better to say a single inverse, I think), lapack_size argument is given here single time. Fourth argument is LDA.
Using LAPACK functions, I calculated the inverse of a matrix, so far. Now, I will multiply the A matrix, which I claim that it is the inverse of the initial matrix, with its initial value where I had saved in matrix B. If it is really inverse of its initial value, I have to come up with identity matrix. BLAS functions have its own naming conventions like LAPACK functions. I used dgemm() for matrix multiplication. It is Double GEneral Matrix Multiplication in short. The line for matrix multiplication is:
Using LAPACK functions, I calculated the inverse of a matrix, so far. Now, I will multiply the A matrix, which I claim that it is the inverse of the initial matrix, with its initial value where I had saved in matrix B. If it is really inverse of its initial value, I have to come up with identity matrix. BLAS functions have its own naming conventions like LAPACK functions. I used dgemm() for matrix multiplication. It is Double GEneral Matrix Multiplication in short. The line for matrix multiplication is:
cblas_dgemm( CblasRowMajor, CblasNoTrans, CblasNoTrans, lapack_size,
lapack_size, lapack_size, 1.0, matrisA, lapack_size, matrisB,
lapack_size, 0.0, matrisC, lapack_size);
There are also predefined values in CBLAS like LAPACK. CblasRowMajor is one of them and its effect is the same as LAPACK_ROW_MAJOR. Two CblasNoTrans argument denote that matrixA and matrixB will be processed as is, respectively. If this argument would be CblasTrans, then the transpose of the corresponding matrix would be processed. In transpose operation, matrix rows become columns and columns become row, so a (m x n) matrix becomes (n x m) after transpose operation. As I mentioned the definition of matrix multiplication, I wrote that only (m x n) sized matrices can be multiplied with (n x p) sized matrices and the product is a (m x p) sized matrix. Three consecutive lapack_size arguments (fourth, fifth and sixth) corresponds to these m, n and p numbers but as we assume m = n = p for simplicity these arguments are all the same.
dgemm does the following operation:
dgemm does the following operation:
| dgemm |
It multiplies A's elements with a alpha scalar, then applies matrix multiplication with B, multiplies C's elements with a beta scalar and sums everything in C. What I want to do is only matrix multiplication, so alpha should be 1.0 and beta should be 0.0. The constant before the argument matrixA is alpha value. The argument lapack_size after matrixA is LDA. After these are the pointer of matrixB and LDB argument of it. And lastly, beta constant with value of 0.0, pointer of matrixC and LDC of matrixC.
References:
References:
I put the function prototypes as comments in the code for simplicity.
gcc matris.c -I/root/lapack-3.8.0/CBLAS/include \
-I/root/lapack-3.8.0/LAPACKE/include -L/root/lapack-3.8.0 \
-llapacke -llapack -lrefblas -lcblas -lgfortran -o matris.x
-I/root/lapack-3.8.0/LAPACKE/include -L/root/lapack-3.8.0 \
-llapacke -llapack -lrefblas -lcblas -lgfortran -o matris.x
The output is following:
The results are completely consistent with the results in GNU Octave:
Appendix: What is LDA and when it is necessary?
This was the LU factorization line:
A matrix = [
0.000000 4.000000 0.000000 ;
3.000000 7.000000 1.000000 ;
5.000000 5.000000 1.000000 ]
post-LU matrixA = [
5.000000 5.000000 1.000000 ;
0.000000 4.000000 0.000000 ;
0.600000 1.000000 0.400000 ]
inverse of A matrix = [
0.250000 -0.500000 0.500000 ;
0.250000 -0.000000 0.000000 ;
-2.500000 2.500000 -1.500000 ]
proof = [
1.000000 -0.000000 0.000000 ;
0.000000 1.000000 0.000000 ;
0.000000 0.000000 1.000000 ]
0.000000 4.000000 0.000000 ;
3.000000 7.000000 1.000000 ;
5.000000 5.000000 1.000000 ]
post-LU matrixA = [
5.000000 5.000000 1.000000 ;
0.000000 4.000000 0.000000 ;
0.600000 1.000000 0.400000 ]
inverse of A matrix = [
0.250000 -0.500000 0.500000 ;
0.250000 -0.000000 0.000000 ;
-2.500000 2.500000 -1.500000 ]
proof = [
1.000000 -0.000000 0.000000 ;
0.000000 1.000000 0.000000 ;
0.000000 0.000000 1.000000 ]
The results are completely consistent with the results in GNU Octave:
I want to rise a notice on the -0's in the output. This is a topic for a future blog post, I want to write about.
Appendix: What is LDA and when it is necessary?
This was the LU factorization line:
LAPACKE_dgetrf(LAPACK_ROW_MAJOR, lapack_boyut, lapack_boyut, matrisA, lapack_boyut, ipiv);
Let's assume there is a relatively big matrix e.g. 20 x 20. I want to process only the sub-matrix with size 5 x 6. A(1:5, 1:6) in Matlab terms. Because this is a part of bigger matrix, the next memory element after the last element of the row (of sub-matrix) is actually not a part of the sub-matrix. Next element of the sub-matrix is actually 20 - 6 = 14 unit (float, complex, etc) away in memory. So, LDA is the difference value between two column-wise consecutive elements in memory. The function should be for this example is:
LAPACKE_dgetrf(LAPACK_ROW_MAJOR, 5, 6, matrisA, 20, ipiv );
To keep this example as simple as it can be, I choose the sub-matrix from upper left. Otherwise I would have to deal with some pointer arithmetic operations to find out the memory address of the first element in matrix A. There is one more thing to be considered. LDA denotes the distance between two consecutive column elements because LAPACK_ROW_MAJOR is given. If it would be LAPACK_COL_MAJOR then LDA has to be the distance between two consecutive row elements. In short, LDA has to be the row or the column number of the original matrix while working on sub-matrices. LAPACK_ROW_MAJOR or LAPACK_COLUMN_MAJOR determines the value as row or column.

No comments:
Post a Comment